MVOCC vs. SVOCC: A Comprehensive Guide to Optimistic Concurrency Control

This blog begins by introducing key theorems related to serializability. These theorems are then used to explain the three conditions applied in single-version OCC, which form the foundation for implementing the validation phase. Finally, we explore multi-version OCC and discuss its advantages over the single-version approach.

Basics of Optimistic Concurrency Control

OBSERVATIONS ON OPTIMISTIC CONCURRENCY CONTROL SCHEMES describes OCC as follows:

When transactions are accessing a database concurrently, a concurrency control (CC) scheme has to prevent conflicts among them such that their serializability can be guaranteed.

Conventional CC schemes use two-phase locking protocols acquiring dynamically locks for the objects.

Optimistic CC schemes are designed to get rid of the locking overhead. The burden of CC is deferred unitl EOT when some checking for potential conflicts has to take place. If a conceivable conflict is detected, a "pessimistic" view has to be taken: this conceivable conflict is resolved by aborting the transaction. Hence, theses schemes rely on transaction backout as a control mechanism.

Serialization Graphs and Conflict-Serializability

Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions provides a generalized theory about OCC. Since the original paper spans 198 pages, this section summarizes critical aspects related to serializability (with some simplifications for clarity):

A history $H$ represents a set of transactions, described as a partial order of events $E$ that reflect the operations (such as reads, writes, commits, and aborts) of the transactions.
The direct serialization graph $\operatorname{DSG}(H)$ of a given history $H$ is a graph constructed as follows:
- Each node in $\operatorname{DSG}(H)$ corresponds to a committed transaction in $H$.
- Directed edges correspond to different types of direct conflicts.
  - Directly item-read-depends: $T_j$ directly item-read-depends on $T_i$ if $T_i$ installs some object version $x_i$ and $T_j$ reads $x_i$.
  - Directly item-anti-depends: $T_j$ directly item-anti-depends on transaction $T_i$ if $T_i$ reads some object version $x_k$ and $T_j$ installs $x$'s next version (after $x_k$).
  - Directly item-write-depends: $T_j$ directly item-write-depends on transaction $T_i$ if $T_i$ installs a version $x_i$ and $T_j$ installs $x$'s next version (after $x_i$).
The graph $\operatorname{DSG}(H)$ is acyclic, and aborted reads (where a transaction reads a version written by an aborted transaction) and intermediate reads (where a transaction reads a version that is not the final version written by a committed transaction) are proscribed for a history $H$ iff $H$ is conflict-serializable.

The above description of serialization graphs and conflict-serializability is a simplified and informal explanation. It omits several key aspects for the sake of clarity, such as the inclusion of the version order as part of the history and the need to account for predicate-based dependencies arising from scanning operations. Additionally, the proof that the acyclicity of the direct serialization graph ($\operatorname{DSG}(H)$) implies conflict-serializability is not provided here. The following references provide the necessary foundational details and formal arguments to address the aspects omitted in the simplified description above:

Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions
The Wormhole Theorem, as described in section 7.5.8.1 of "Transaction Processing: Concepts and Techniques" by J. N. Gray and A. Reuter (Morgan Kaufmann Publishers Inc., 1993)
The Serializability Theorem, as described in Section 2.3 of "Concurrency Control and Recovery in Database Systems" by Philip A. Bernstein, Vassos Hadzilacos, and Nathan Goodman

Cycle Prevention with Timestamps

Since the acyclicity of the direct serialization graph ($\operatorname{DSG}(H)$) implies conflict-serializability, OCC only needs to detect cycles and abort transactions that could introduce cycles. However, detecting cycles using traditional graph algorithms can be computationally expensive, as it requires each machine to have a complete view of the graph.

To overcome this, we can leverage logical clocks (timestamps) to enforce a one-directional dependency graph, which guarantees acyclicity. The idea is simple: assign each transaction a logical timestamp, and enforce a rule where a transaction can only depend on another transaction with a smaller timestamp. This ensures that all dependencies flow in one direction, thereby preventing cycles.

Backward and Forward Validation

OBSERVATIONS ON OPTIMISTIC CONCURRENCY CONTROL SCHEMES proposes two methods for detecting wrong-direction dependencies:

Backward oriented optimistic CC (BOCC) checks during the validation phase of $T_j$ whether its read set $\operatorname{RS}(T_j)$ intersects with any of the write sets $\operatorname{WS}(T_i)$ of all concurrently executed transactions $T_i$ having finished their read phases before $T_j$. Since "blind" modifications are not very likely, each transaction has to be validated in practice.

Let $T_{start}$ be the highest transaction number assigned to some transaction when $T_j$ starts, and $T_{finish}$ the highest transaction number when $T_j$ enters its validation phase. Then, essentially the following procedure in $T_j$'s validation phase will decide $T_j$'s destiny.
1
2
3
4
5
6
VALID := TRUE;
FOR T(i) := T(start+1) TO T(finish) DO
  IF RS(T(j)) \intersect WS(T(i)) != \emptyset THEN
    VALID := FALSE;
IF VALID THEN COMMIT
         ELSE ABORT;
Forward oriented optimistic CC (FOCC) checks during the validation phase of $T_j$ whether its write set $\operatorname{WS}(T_j)$ intersects with any of the read sets $\operatorname{RS}(T_i)$ of all transactions $T_i$ having not yet finished their read phases.

Let the active transactions have the numbers $T_{act1}$ until $T_{actn}$. Then, $T_j$ is validated as follows:
1
2
3
4
5
6
VALID := TRUE;
FOR T(i) := T(act1) TO T(actn) DO
  IF WS(T(j)) \intersect RS(T(i)) != \emptyset THEN
    VALID := FALSE;
IF VALID THEN COMMIT
         ELSE ABORT;

It is important to note that the paper assumes blind writes are not possible, meaning the write set of a transaction is a superset of its read set. As a result, if transaction $T_j$ item-write-depends on transaction $T_i$, then $T_j$ also item-anti-depends on $T_i$. Consequently, there is no need to explicitly test for wrong-direction item-write-dependencies during backward validation.

Both backward-oriented and forward-oriented optimistic CC (also known as backward validation and forward validation) can detect and prevent wrong-direction dependencies. While the formal proof is omitted here, the intuition is as follows, assuming Jack and Tom want to enter two lines:

Backward validation is like Jack entering a line where no one ahead of him promises not to harm him if he enters. Jack himself makes no promises to those behind him. The only thing Jack needs to do is check whether anyone ahead could potentially harm him. If so, he leaves (the transaction aborts); otherwise, he stays in line (the transaction commits).
Forward validation is like Tom entering a line where those ahead have promised not to harm him, and Tom himself promises not to harm anyone behind him. Tom's job is to check if anyone behind him might be affected if he stays. If so, he leaves (the transaction aborts); otherwise, he stays (the transaction commits).

However, backward validation is more commonly used, so we will focus on it. In backward validation, a transaction is validated by checking it against other concurrent transactions (transactions whose lifetimes overlap) with smaller timestamps. The assignment of timestamps and the timing of validation are crucial and must be coordinated to ensure that, once Jack decides to stay in line (i.e., the transaction commits), no one who was not already in the queue (i.e., not assigned a timestamp already) before validation can queue ahead of him afterward (i.e., be assigned a smaller timestamp).

Single-Version Optimistic Concurrency Control

Single-version OCC is a straightforward approach to implementing optimistic concurrency control. In this context, "single-version" means that, globally, there is at most one version of each object available to all transactions. While a transaction may create local copies of objects in its own workspace during execution, these local versions are private and cannot be accessed by other transactions until the transaction commits.

Phases of a Transaction in SVOCC

On Optimistic Methods for Concurrency Control introduces a method where a transaction is divided into three phases:

It is required that any transaction consist of two or three phases: a read phase, a validation phase, and a possible write phase (see Figure 1).

During the read phase, the transaction reads the data and locally stores any changes it intends to make. Importantly, no changes are written to the global database during this phase. All modifications are made on local copies of the data.
If validation is successful, the transaction enters the write phase, wherein the local changes are applied to the global database.

Local Writes in Active Transactions

On Optimistic Methods for Concurrency Control emphasizes that no global modifications occur during the read phase of a transaction:

During the read phase, all writes take place on local copies of the nodes to be modified. Then, if it can be established during the validation phase that the changes the transaction made will not cause a loss of integrity, the local copies are made global in the write phase.

This is the simplest way to avoid aborted reads and intermediate reads.

The Validation Phase

Choosing the Timing for Timestamp Assignment

The following statements are quoted from On Optimistic Methods for Concurrency Control:

In order to verify (1), a permutation $\pi$ must be found. This is handled by explicitly assigning each transaction $T_i$, a unique integer transaction number $t(i)$ during the course of its execution.

On first thought, we might assign transaction numbers at the beginning of the read phase; however, this is not optimistic (hence contrary to the philosophy of this paper) for the following reason. Consider the case of two transactions, $T_1$ and $T_2$, starting at roughly the same time, assigned transaction number $n$ and $n + 1$, respectively. Even if $T_2$ completes its read phase much earlier than $T_1$, before being validated $T_2$ must wait for the completion of the read phase of $T_1$, since the validation of $T_2$ in this case relies on knowledge of the write set of $T_1$ (see Figure 3).

In an optimistic approach, we would like for transactions to be validated immediately if at all possible (in order to improve response time). For these and similar considerations we assign transaction numbers at the end of the read phase.

Although the paper states that "before being validated $T_2$ must wait for the completion of the read phase of $T_1$," I believe this is a limitation of using backward validation in isolation. Combining backward validation with forward validation can address this issue. However, let's follow the paper in the discussion below.

Three Conditions for Validation

On Optimistic Methods for Concurrency Control proposes three conditions to validate transactions:

There must exist a serially equivalent schedule in which transaction $T_i$ comes before transaction $T_j$ whenever $t(i)$ < $t(j)$. This can be guaranteed by the following validation condition: for each transaction $T_j$ with transaction number $t(j)$, and for all $T_i$ with $t(i) < t(j)$; one of the following three conditions must hold (see Figure 2):

$T_i$ completes its write phase before $T_j$ starts its read phase.

The write set of $T_i$ does not intersect the read set of $T_j$, and $T_i$ completes its write phase before $T_j$ starts its write phase.

The write set of $T_i$ does not intersect the read set or the write set of $T_j$, and $T_i$ completes its read phase before $T_j$ completes its read phase.

These three conditions are essential in the backward validation to ensure that no cycles form in the direct serialization graph. The following table shows how the three conditions prevent different types of dependencies with wrong direction:

Condition	Is $T_i$ item-read-depends on $T_j$ possible?	Is $T_i$ item-anti-depends on $T_j$ possible?	Is $T_i$ item-write-depends on $T_j$ possible?
(1)	No: $T_i$ completes before $T_j$ starts, so $T_i$ cannot read any versions written by $T_j$.	No: $T_j$ starts after $T_i$ completes, so $T_j$ either reads the version written by $T_i$ or a newer version. It cannot read an older version.	No: $T_i$ completes its write phase before $T_j$ starts writing, so only $T_j$ can overwrite $T_i$'s version. The reverse is impossible.
(2)	No: $T_i$ completes its write phase before $T_j$ starts writing, so $T_i$ completes its read phase before $T_j$ starts writing. Therefore, $T_i$ cannot read any version written by $T_j$.	No: The write set of $T_i$ does not intersect the read set of $T_j$, so what $T_j$ reads cannot be overwritten by $T_i$.	No: $T_i$ completes its write phase before $T_j$ starts writing, so only $T_j$ can install the next version. The reverse is not possible.
(3)	No: $T_i$ completes its read phase before $T_j$ completes its read phase, which means $T_i$ also completes its read phase before $T_j$ starts its write phase. Therefore, $T_i$ cannot read what $T_j$ writes.	No: The read set of $T_j$ does not intersect the write set of $T_i$, so $T_j$ cannot read any version written by $T_i$.	No: The write set of $T_j$ does not intersect the write set of $T_i$, so neither transaction can overwrite the other's version.

The above explanation omits some details for the sake of clarity. For example, Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions emphasizes that the version order in a history $H$ can be different from the order of write or commit events in $H$. However, for simplicity, we assume here that the version order of involved objects corresponds directly to the commit event order. Additionally, we do not cover more advanced topics such as scanning operations and predicate-based dependencies.

Serial Validation

The following code is quoted from On Optimistic Methods for Concurrency Control:

tbegin = (
  create set := empty;
  read set := empty;
  write set := empty;
  delete set := empty;
  start tn := tnc)
tend = (
  // The part enclosed by < and > represents a critical section,
  // which functions similarly to a mutex guard.
  <finish tn := tnc;
   valid := true;
   for t from start tn + 1 to finish tn do
     if (write set of transaction with transaction number t intersects read set)
       then valid:= false;
   if valid
     then ((write phase); tnc := tnc + 1; tn := tnc)>;
  if valid
    then (cleanup)
    else (backup)).

My understanding of the above code can be split into three parts: validating the transaction with transactions whose tn is smaller than or equal to start tn, from start tn + 1 to finish tn, and larger than finish tn:

The write phase and the increment of the tnc are performed as a single atomic action within the same critical section. This ensures that all transactions with a tn less than the current transaction's start tn have already completed their write phase before the current transaction starts its read phase. During the validation phase of the current transaction, these earlier transactions (with a tn less than the current transaction's start tn) can be handled using Condition (1), meaning their read and write sets do not need to be explicitly checked with the current transaction's read and write sets - they naturally pass the validation.
The write phase and the increment of the tnc are executed as a single atomic action within the same critical section. Since the critical section is executed for multiple transactions one by one, this guarantees that transactions with smaller tn complete their write phase before transactions with larger tn start their write phase. As a result, this satisfies part of Condition (2), allowing us to use Condition (2) to validate transactions from start tn + 1 to finish tn.
The validation phase, the increment of the tnc, and the assignment of the incremented tnc to the transaction's tn are performed as a single atomic action within the same critical section. This ensures that after the validation phase of the current transaction, no transaction that hasn't yet been assigned a tn before the current transaction's validation phase will be assigned a smaller tn than the current transaction's tn.
- Using the analogy used before: After Jack decides to stay in line (i.e., the current transaction passes the validation check and commits), no one who was not already in the queue (i.e., no transaction without a tn before the current transaction's validation phase) can jump ahead of him (i.e., can be assigned a smaller tn than Jack's).
- This is an example of how the assignment of timestamps and the timing of validation are crucial and must be coordinated, as mentioned previously.
- Notice: In backward validation, for transactions with a tn larger than the current transaction's tn, it is their responsibility to validate whether they violate serializability with the current transaction - not the current transaction's responsibility.

Parallel Validation

The following code is quoted from On Optimistic Methods for Concurrency Control:

tend = (
  // Critical section A.
  <finish tn := tnc;
   finish active := (make a copy of active);
   active := active \union {id of this transaction}>;
  valid := true;
  for t from start tn + 1 to finish tn do
    if (write set of transaction with transaction number t intersects read set)
      then valid := false;
  for i \in finish active do
    if (write set of transaction Ti intersects read set or write set)
      then valid := false;
  if valid
    then (
      (write phase);
      // Critical section B.
      <tnc := tnc + 1;
       tn := tnc;
       active := active - {id of this transaction}>;
      (cleanup))
    else (
      // Critical section C.
      <active := active - {id of transaction}>;
      (backup))).

My understanding of the above code is as follows:

The three critical sections, A, B, and C, share the same mutex. At any given time, only one critical section can be executing.
While validating the current transaction in critical section A, the transactions with tn between start tn + 1 and finish tn have already completed their write phases and have been assigned a tn in critical section B (otherwise, these transactions would have a tn larger than finish tn; the critical section A of the current transaction is exclusive with the critical section B of those transactions - they cannot execute concurrently, and one must occur before the other). This ensures that their write phases are completed before the current transaction starts its own write phase, allowing us to apply Condition (2) for their validation. This mirrors the behavior of serial validation.
When the current transaction obtains finish active by copying active in critical section A, it has just completed its read phase and has not yet started its write phase. Meanwhile, all transactions in finish active must have already completed the entire critical section A (otherwise, those transactions would not appear in the finish active set of the current transaction; the critical section A of the current transaction is exclusive with the critical section A of those transactions - they cannot execute concurrently, and one must occur before the other), meaning they completed their read phases before the current transaction completes its read phase or starts its write phase. Therefore, we can apply Condition (3) to validate them.
- Notice: Transactions in the finish active set of the current transaction may enter critical section B either before or after the current transaction, meaning their tn could be smaller or larger than the current transaction's tn. In the case that they are assigned a smaller tn, it is the current transaction's responsibility to check for conflicts with them.
For transactions that haven't been assigned a tn and do not appear in the finish active set of the current transaction, it is their responsibility to check for conflicts with the current transaction. In other words, it is not the current transaction's responsibility to check for conflicts with them.

Multi-Version Optimistic Concurrency Control

Designing an MVOCC Protocol Based on SVOCC

Basic Storage Format of Versions

In a MVOCC protocol, multiple versions of the same object must explicitly declare the lifecycle of each version. This is achieved by introducing a Begin field and an End field, which define the lifetime of each version. (Note that the Begin and End fields are distinct from the begin timestamp and end timestamp mentioned below; both the Begin field and the End field in the version record correspond to the end timestamp of a transaction.) Together with the original columns, these fields construct the record format for each version.

Begin	End	Name	Amount
15	inf	Jane	150
10	20	John	100
20	Txn75	John	110
Txn75	inf	John	130
30	Txn75	Larry	170
Txn75	inf	Larry	150

Why Two Timestamps Are Needed in MVOCC

High-Performance Concurrency Control Mechanisms for Main-Memory Databases assigns two timestamps to a transaction:

Begin Timestamp: Acquired at the start of the transaction.
End Timestamp: Acquired when the transaction is ready to be validated.

Transaction 75 is in the process of transferring $20 from Larry's account to John's account. It has created the new versions for Larry (Larry, 150) and for John (John, 130) and inserted them into the appropriate buckets in the index.

Note that transaction 75 has stored its transaction ID in the Begin and End fields of the new and old versions, respectively. (One bit in the field indicates the field's current content.)

Now suppose transaction 75 commits with end timestamp 100. It then returns to the old and new versions and sets the Begin and End fields, respectively, to 100. The final values are shown in red below the old and new versions. The old version (John, 110) now has the valid time 20 to 100 and the new version (John, 130) has a valid time from 100 to infinity.

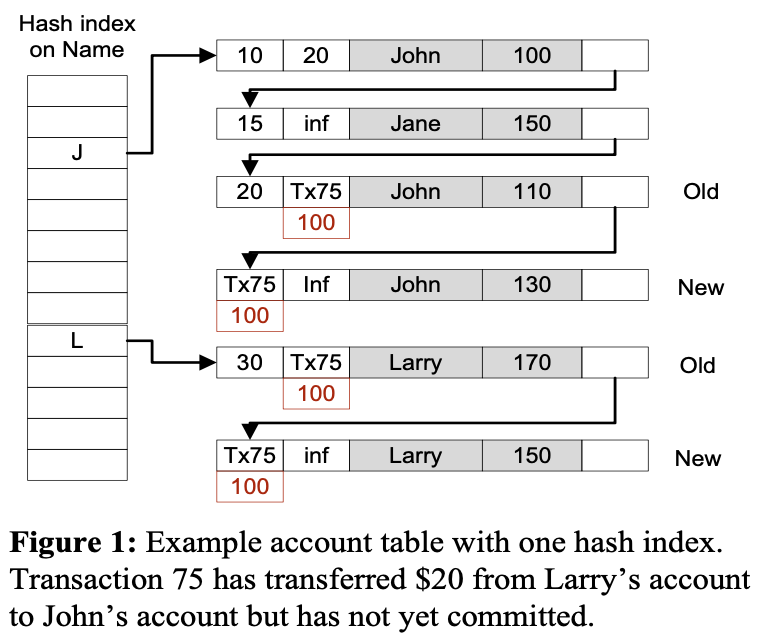
Figure 1: Example account table with one hash index. Transaction 75 has transferred $20 from Larry's account to John's account but has not yet committed.

In my view, the end timestamp in High-Performance Concurrency Control Mechanisms for Main-Memory Databases corresponds to the transaction number in On Optimistic Methods for Concurrency Control. Both papers opt to assign the end timestamp or transaction number at the end of the read phase to allow transactions to be validated immediately, rather than having to wait for transactions with smaller end timestamps or transaction numbers that have not yet completed their read phase.

Additionally, an MVOCC transaction requires a timestamp during the read phase to identify the correct version of an object. This timestamp is the begin timestamp. This is why High-Performance Concurrency Control Mechanisms for Main-Memory Databases assigns two timestamps to each transaction.

However, in my opinion, the requirement that "before being validated $T_2$ must wait for the completion of the read phase of $T_1$" is a limitation of relying solely on backward validation. I believe that combining backward validation with forward validation could resolve this issue, allowing the end timestamp or transaction number to be assigned at the start of the transaction, thereby eliminating the need for two timestamps in MVOCC. That said, I am still in the process of proving this hypothesis.

How Active Transactions Write Objects with New Versions

Due to the presence of Begin and End fields indicating the lifecycle of each version, MVOCC allows global modifications to occur even during the read phase of a transaction, unlike SVOCC. High-Performance Concurrency Control Mechanisms for Main-Memory Databases provides an example of a bank transfer:

Transaction 75 is in the process of transferring $20 from Larry's account to John's account. It has created the new versions for Larry (Larry, 150) and for John (John, 130) and inserted them into the appropriate buckets in the index.

Note that transaction 75 has stored its transaction ID in the Begin and End fields of the new and old versions, respectively. (One bit in the field indicates the field's current content.)

Begin	End	Name	Amount
15	inf	Jane	150
10	20	John	100
20	Txn75	John	110	Old
Txn75	inf	John	130	New
30	Txn75	Larry	170	Old
Txn75	inf	Larry	150	New

In the read phase of transaction 75, a new version is created globally. Unlike SVOCC, making global modifications during the read phase of transaction 75 does not result in aborted reads or intermediate reads. This is because the system records the transaction ID, rather than a timestamp, in the End field of the old version and the Begin field of the new version. As a result, other transactions either ignore these in-progress versions or wait for transaction 75 to commit before they proceed with their own commits.

Moreover, making global modifications offers an advantage: it reduces the transaction abortion rate, as will be demonstrated in a later section.

How to Locate a Specific Version When Reading an Object

Essentially, a transaction locates a version by finding one where its begin timestamp falls between the Begin and End fields of that version. Building on this, High-Performance Concurrency Control Mechanisms for Main-Memory Databases proposes speculative reads and speculative ignores when encountering a version where either the Begin or End field contains a transaction ID instead of a timestamp (indicating that an ongoing transaction is modifying this version). In this case, the system assumes the ongoing transaction will eventually commit and reads the modifications, creating a commit dependency on the ongoing transaction (i.e., the current transaction must wait for the ongoing transaction to commit before it can commit).

More details can be found in Section 2.5, Version Visibility, of the original paper.

How to Validate and Commit

Essentially, High-Performance Concurrency Control Mechanisms for Main-Memory Databases employs backward validation but optimizes it for in-memory storage:

We use backward validation but optimize it for in-memory storage. Instead of validating a read set against the write sets of all other transactions, we simply check whether a version that was read is still visible as of the end of the transaction.

This blog is designed to omit the discussion on scanning operations. However, if we were to address it, I believe the method High-Performance Concurrency Control Mechanisms for Main-Memory Databases uses to detect anomalies in scanning operations is not entirely accurate. The approach of "T walks its ScanSet and repeats each scan looking for versions that came into existence during T's lifetime and are visible as of the end of the transaction" may not be sufficient. I believe that simply checking if the versions seen during scanning still exist at validation is insufficient. It is also necessary to check if any additional versions appear during validation that were not visible during the read phase. The method proposed in Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions might be more appropriate.

Advantage 1: Lower Abort Rate for Read Transactions

Consider the following sequence of events:

$T_5$ writes $v_5$.
$T_4$ reads $v$.
$T_6$ reads $v$.
$T_5$ commits.
$T_4$ validates.
$T_6$ validates.

In SVOCC, when $T_5$ writes $v_5$, it can either appear in global modification or local modification:

If $v_5$ appears in global modification, then $T_4$ reads $v_5$ and must abort.
If $v_5$ is in local modification, then $T_6$ cannot read $v_5$ and must abort.

Thus, in SVOCC, whether $v_5$ appears in global or local modification, at least one transaction will abort.

In contrast, in MVOCC, $v_5$ can appear in global modification, and:

$T_4$ can read an older version, such as $v_4$, and commit successfully.
$T_6$ can read $v_5$ and commit after $T_5$ commits.

Therefore, MVOCC results in a lower transaction abort rate compared to SVOCC.

Advantage 2: Skipping the Validation Phase for Read Transactions

If a transaction only reads versions whose Begin and End fields are neither inf nor ongoing transaction IDs, and it does not perform any writes, it may be able to commit directly without undergoing a validation phase. For example, consider a transaction with a begin timestamp of 50 that reads the following data:

Begin=10, End=100, Name=John, Amount=100
Begin=30, End=100, Name=Larry, Amount=170

Begin	End	Name	Amount
15	inf	Jane	150
10	20	John	100
20	100	John	110
100	inf	John	130
30	100	Larry	170
100	inf	Larry	150

Reference

Computer Science > Serializability

MVOCC vs. SVOCC: A Comprehensive Guide to Optimistic Concurrency Control

https://clcanny.github.io/2024/10/26/computer-science/serializability/mvocc-vs-svocc-a-comprehensive-guide-to-optimistic-concurrency-control/

作者

JunBin

发布于

2024年10月26日

许可协议

FalconFS: Trading Rename Performance for Single-Hop Operations at Scale 上一篇

Design Document: DataNode for Distributed Filesystem 下一篇

Condition	Is \(T_i\) item-read-depends on \(T_j\) possible?	Is \(T_i\) item-anti-depends on \(T_j\) possible?	Is \(T_i\) item-write-depends on \(T_j\) possible?
(1)	No: \(T_i\) completes before \(T_j\) starts, so \(T_i\) cannot read any versions written by \(T_j\).	No: \(T_j\) starts after \(T_i\) completes, so \(T_j\) either reads the version written by \(T_i\) or a newer version. It cannot read an older version.	No: \(T_i\) completes its write phase before \(T_j\) starts writing, so only \(T_j\) can overwrite \(T_i\)'s version. The reverse is impossible.
(2)	No: \(T_i\) completes its write phase before \(T_j\) starts writing, so \(T_i\) completes its read phase before \(T_j\) starts writing. Therefore, \(T_i\) cannot read any version written by \(T_j\).	No: The write set of \(T_i\) does not intersect the read set of \(T_j\), so what \(T_j\) reads cannot be overwritten by \(T_i\).	No: \(T_i\) completes its write phase before \(T_j\) starts writing, so only \(T_j\) can install the next version. The reverse is not possible.
(3)	No: \(T_i\) completes its read phase before \(T_j\) completes its read phase, which means \(T_i\) also completes its read phase before \(T_j\) starts its write phase. Therefore, \(T_i\) cannot read what \(T_j\) writes.	No: The read set of \(T_j\) does not intersect the write set of \(T_i\), so \(T_j\) cannot read any version written by \(T_i\).	No: The write set of \(T_j\) does not intersect the write set of \(T_i\), so neither transaction can overwrite the other's version.