Design Document: Enhancing Inode Attributes and Storage Policies in HDFS

Background: HDFS Solutions and Implementation for Archival Storage

Apache Hadoop 3.3.6 > Archival Storage, SSD & Memory introduces archival storage to decouple storage capacity from compute capacity:

Archival Storage is a solution to decouple growing storage capacity from compute capacity. Nodes with higher density and less expensive storage with low compute power are becoming available and can be used as cold storage in the clusters. Based on policy the data from hot can be moved to the cold. Adding more nodes to the cold storage can grow the storage independent of the compute capacity in the cluster.

Archival storage consists of two key components:

1. Storage Policy Resolution: Determines the storage policy for files (e.g., hot, cold, warm, all SSD, one SSD).
2. Data Movement: Ensures data is relocated to match the storage policy, addressing any discrepancies between expected and actual storage locations.

Apache Hadoop 3.3.6 > Archival Storage, SSD & Memory and Storage-Policy-Satisfier-in-HDFS-Oct-26-2017.pdf highlight two scenarios requiring data movement:

1. Setting a new storage policy on already existing file/dir will change the policy in Namespace, but it will not move the blocks physically across storage medias.
2. Other scenario is, when user rename the files from one affected storage policy file (inherited policy from parent directory) to another storage policy effected directory, it will not copy inherited storage policy from source. So it will take effect from destination file/dir parent storage policy. This rename operation is just a metadata change in Namenode. The physical blocks still remain with source storage policy.

Storage policy resolution is straightforward:

The effective storage policy of a file or directory is resolved by the following rules.

1. If the file or directory is specified with a storage policy, return it.
2. For an unspecified file or directory, if it is the root directory, return the default storage policy. Otherwise, return its parent's effective storage policy.

Users have two options to move blocks according to a new policy. The first option is the HDFS-10285: Storage Policy Satisfier in HDFS. The following figures illustrate the basic workflow of SPS:

Fig-1: Namenode extensions

Fig-2: Coordinatingblocksmovement using C-DN

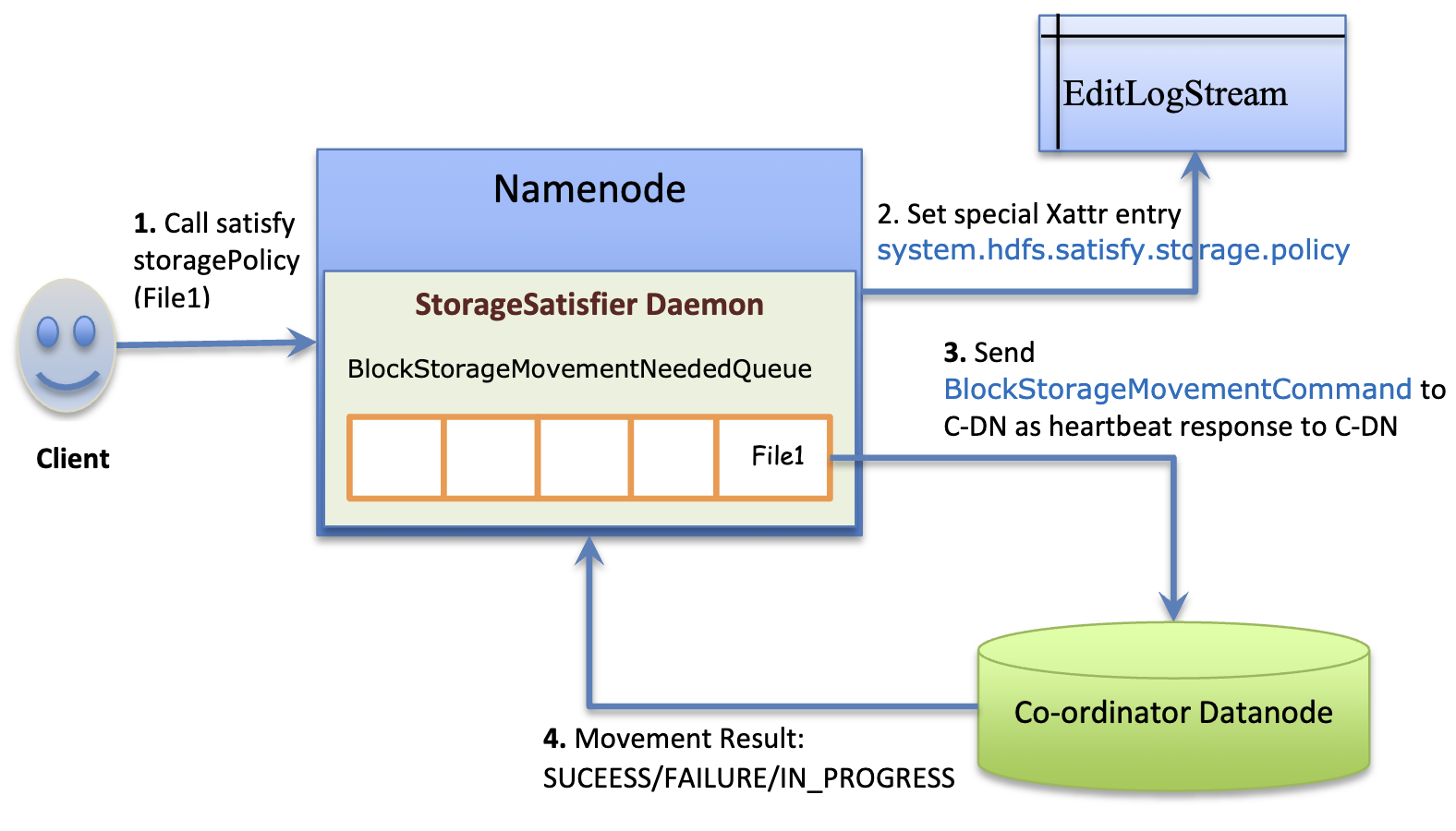
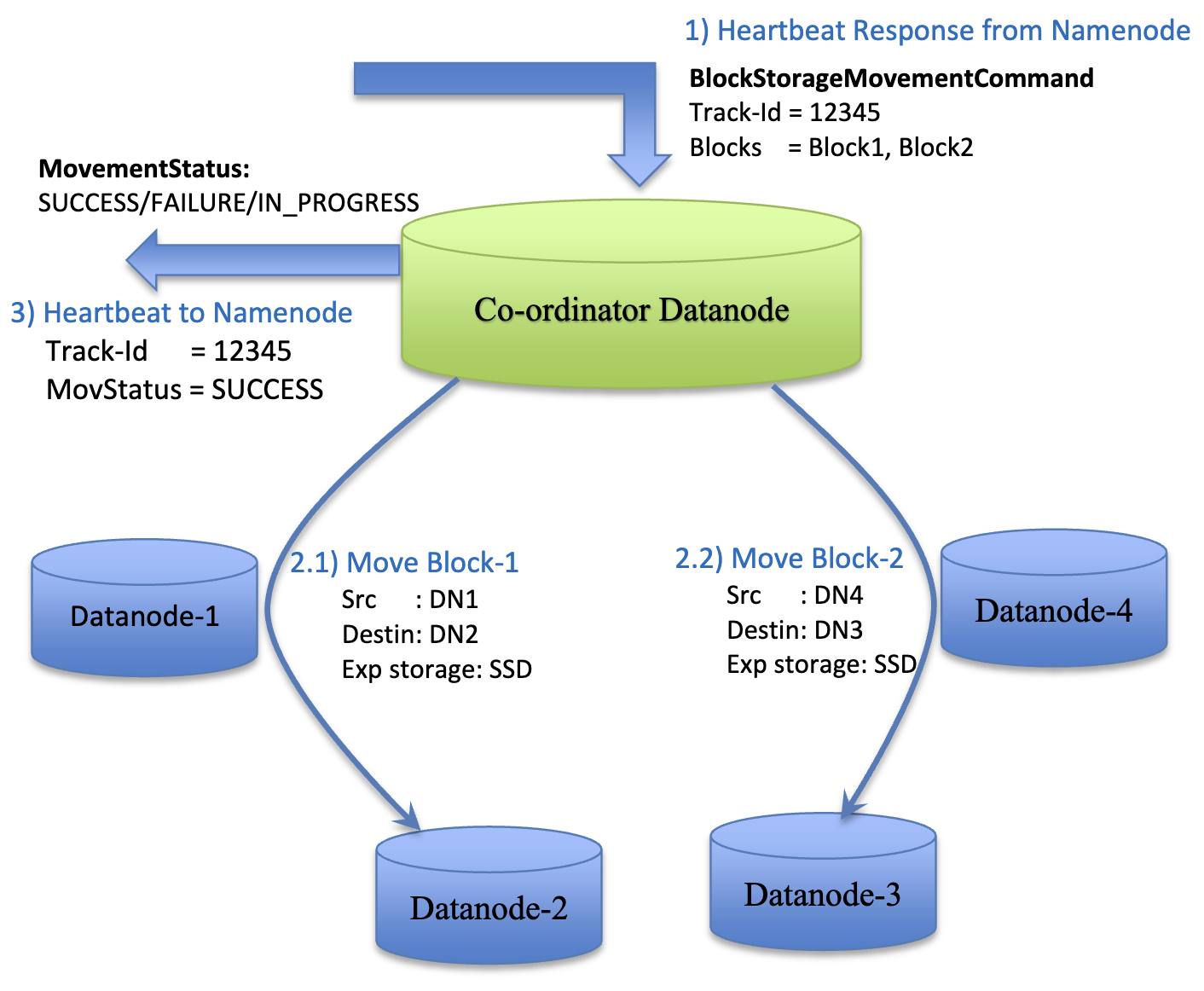
The primary responsibility of the NameNode extensions is to recursively scan all files within a user-specified directory and connect with the Coordinator DataNode using the BlockStorageMovementCommand. The details are illustrated in Storage-Policy-Satisfier-in-HDFS-Oct-26-2017.pdf:

If the source path is a directory then all the files under the directory recursively would be considered for satisfying the policy. All the submitted directory inodes will be tracked separately at queue BlockStorageMovementNeeded#spsDirsToBeTraversedLater, these directories will be asynchronously traversed and all the file inodes under each directory will be added to the queue BlockStorageMovementNeeded#storageMovementNeeded. There could be a case of large directory, which can have several files under it. Here, traversing all files and collecting Inodes would be time consuming and its not recommended to hold Namenode locks longer time until the directory is fully scanned. Again, this could increase memory consumption if we keep lot of files inode into memory. To avoid these issues, SPS will throttle itself and traverse the directories in batch wise. Added a limit of 1000 size to the queue storageMovementNeeded. If storageMovementNeeded becomes full with 1000 elements, directory traversal will be suspended until storageMovementNeeded has some free slots available, lower than 1000. When scan was suspended, it releases the Namenode lock, so that other Namenode operations will not be blocked.

Limitations in Xattr Resolution and Improvements

In general, we not only consider storage policy as a standalone concept but treat it as a type of xattr. The following section discusses xattrs in this broader context.

Current Limitations in Xattr Resolution

In HDFS, the biggest shortcoming of storage policy resolution is its counter-intuitive nature. Consider this example, where TxID (transaction ID) represents the logical clock for capturing "happen-before" relationships - transactions with smaller TxID values occur before those with larger ones:

• Operations:
  • [TxID=1] Set storage policy to "hot" on directory /a/b.
  • [TxID=2] Set storage policy to "all ssd" on directory /a.
• Result: The file /a/b/c unexpectedly retains the "hot" storage policy, even when the policy for the entire /a directory is reset. Let's take the Linux chown command as an example. In Linux, if a user executes chown -R on /a, it may not affect /a/b/c if chown -R was previously executed on /a/b. This behavior can seem unexpected and counter-intuitive.

Desired Behavior for Xattr Resolution

Let's define the following terms for our discussion:

• Immediate Parent (or Parent): /a is the immediate parent of /a/b, but not of /a/b/c.
• Ancestor: Both /a and /a/b are ancestors of /a/b/c.
• Immediate Child (or Child): /a/b is the immediate child of /a, but /a/b/c is not.
• Descendant: Both /a/b and /a/b/c are descendants of /a.
• Non-inherited Xattr: When an xattr is set on /a, only /a is affected; its descendants are not.
• Inherited Xattr: When an xattr is set on /a, it also affects the xattrs of /a's descendants.
• Rename Affected Inherited Xattr: When /a/c is renamed to /b/c, /b/c's xattr aligns with /b instead of retaining its original xattr.
• Non-rename Affected Inherited Xattr: When /a/c is renamed to /b/c, /b/c retains its original xattr without change.

In this section, we focus on inherited xattrs. The implementation of non-inherited xattrs is straightforward and not worth discussing in detail. Below, we explore the desired behavior for inherited xattrs. Let's define what kind of xattr resolution is intuitive and straightforward:

• Imagine a "magician" who can instantly modify the xattr of the target inode and all its descendant inodes.
• Each inode's xattr is determined by the most recent operation applied to it.

Illustration of Intuitive Rename Affected Inherited Xattr Resolution

The graph above illustrates how the "magician" handles rename affected inherited xattr:

• In TxID 1, a and all its descendants are set to blue when the user sets /a to blue.
• In TxID 3, d inherits the blue xattr from its destination parent.

Illustration of Intuitive Non-rename Affected Inherited Xattr Resolution

The graph above illustrates how the "magician" handles non-rename affected inherited xattr. It is similar to rename affected inherited xattr, but with one key difference: when /a/b is renamed to /a/c/b, b and its descendant inodes retain their original xattrs.

Implementation Outline for Improved Resolution

Rename Affected Inherited Xattr

Let's discuss the rename affected inherited xattr first. We define the following symbols to aid our discussion:

• \(\operatorname{TxID}(\text{node}, \text{setxattr})\): The transaction ID when xattr is set on \(\text{node}\).
• \(\operatorname{TxID}(\text{node}, \text{renamed})\): The transaction ID when \(\text{node}\) is renamed.
• \(\operatorname{TxID}(\text{node})\): The transaction ID that determines the xattr of \(\text{node}\).

There are three operations for a node: create, rename, and delete. We'll focus on the most complex operation, rename.

To simplify the process, imagine that a setxattr event always accompanies a rename event. For example, when [TxID=3] renames /a/b/d to /a/c/d, it also generates a setxattr event [TxID=3] to set /a/c/d's xattr to /a/c's xattr. This introduces a constraint: \(\operatorname{TxID}(\text{node}, \text{setxattr}) \ge \operatorname{TxID}(\text{node}, \text{renamed})\).

Now, let's denote the node we are calculating as \(\text{self}\) and its parent as \(\text{parent}\). There are three cases to consider:

• \(\operatorname{TxID}(\text{parent}) > \operatorname{TxID}(\text{self}, \text{setxattr}) \ge \operatorname{TxID}(\text{self}, \text{renamed})\): This means that \(\text{self}\) was first moved into \(\text{parent}\), then \(\text{parent}\) or its ancestors had their xattr set by a user's direct setxattr request or an accompanying event triggered by a user's rename request. The xattr should be determined by the parent's xattr. This is correct because the event at \(\text{parent}\) or its ancestors is more recent.
• \(\operatorname{TxID}(\text{self}, \text{setxattr}) > \operatorname{TxID}(\text{parent}) > \operatorname{TxID}(\text{self}, \text{renamed})\): Here, \(\text{self}\) is renamed into \(\text{parent}\), then the ancestor's xattr is set, and finally, \(\text{self}\)'s xattr is set. The xattr should be determined by the setxattr event on \(\text{self}\). This is straightforward.
• \(\operatorname{TxID}(\text{self}, \text{setxattr}) \ge \operatorname{TxID}(\text{self}, \text{renamed}) > \operatorname{TxID}(\text{parent})\): The xattr should be determined by the setxattr event on \(\text{self}\). This is also straightforward.

The above three cases can be simplified to two:

• \(\operatorname{TxID}(\text{parent}) > \operatorname{TxID}(\text{self}, \text{setxattr})\): The xattr should be determined by the parent's xattr.
• \(\operatorname{TxID}(\text{self}, \text{setxattr}) > \operatorname{TxID}(\text{parent})\): The xattr should be determined by the setxattr event on \(\text{self}\).

Interestingly, we find that we don't need to record \(\operatorname{TxID}(\text{self}, \text{renamed})\) because it is unnecessary. The xattr of \(\text{self}\) is determined by the maximum \(\operatorname{TxID}(\text{node}, \text{setxattr})\), where \(\text{node}\) is \(\text{self}\) or its ancestors.

Non-rename Affected Inherited Xattr

In discussing non-rename affected inherited xattrs, we encounter more complexity compared to rename-affected inherited xattrs. The following two graphs illustrate these complexities. Notice that the color represents the expected xattr (also referred to as the "magician" xattr), while the actual xattr of each node is indicated by text.

Illustration for Tracking TxIDs in Xattr Resolution (Graph 1)

In Graph 1, at TxID 6, the expected xattr of d is not influenced by its parent c, because d was renamed after c set its xattr. Conversely, e's expected xattr is affected by its parent c since it was renamed before c's setxattr. At TxID 7, when e's xattr is set, it is no longer influenced by its parent. Therefore, the expected xattr is calculated using its rename TxID, setxattr TxID, and its parent's setxattr TxID.

Illustration for Tracking TxIDs in Xattr Resolution (Graph 2)

In Graph 2, TxID 6 shows a rename operation. When renaming d:

• d should inherit the actual xattr blue from its source parent c. Otherwise, if its actual xattr remains white after renaming, the expected xattr for d and its children cannot be calculated.
• Naturally, d should also inherit the setxattr TxID from its source parent c.
  • One way to think about this is that when setxattr was applied to c at TxID 3, the "magician" set all of its descendants' setxattr TxID to 3 at that moment. To avoid losing this information during renaming, d should inherit the TxID from its parent.
  • Another perspective is that d's setxattr TxID should be greater than e's setxattr TxID (2) and smaller than f's setxattr TxID (4), which can only be 3. Otherwise, at least one of d's children's xattrs cannot be calculated.

Combining insights from Graph 1 and Graph 2, the algorithm for calculating non-rename affected inherited xattrs becomes clear:

• Compare the inode's setxattr TxID, rename TxID, and the parent's setxattr TxID to determine the inode's xattr. Recursively apply this process up to the root.
• When a rename occurs, the renamed inode should inherit the setxattr TxID and xattr from its ancestors if necessary. The setxattr TxID should be from the ancestor whose setxattr influences the renamed inode's xattr. Similarly, the xattr should be from the ancestor whose setxattr affects the renamed inode's xattr.

Formal Verification with TLA+

In the following TLA+ specification, we do not use natural numbers as TxIDs for rename and setxattr operations. Instead, we use a variable modOrder to capture the "happens-before" relationship of operations. This approach reduces the number of states TLA+ needs to calculate, as the specific TxID values become irrelevant. For example, the setxattr of a and b at TxIDs 1 and 3, or at 2 and 4, are considered identical when using modOrder.

---------------------------------------- MODULE Xattr ----------------------------------------
EXTENDS Naturals, Sequences, TLC
CONSTANTS root, inodes, null, values, rename, setxattr, operations

ASSUME
  /\ root \notin inodes
  /\ null \in values
  /\ operations = {rename, setxattr}

VARIABLES parent,
          expRenAffXattr, actRenAffXattr,
          expNonRenAffXattr, actNonRenAffXattr,
          modOrder
SYMM == Permutations(inodes) \union Permutations(values \ {null})

\* Utility Operations.
Min(set) == CHOOSE x \in set: \A y \in set: x <= y
Max(set) == CHOOSE x \in set: \A y \in set: x >= y
RECURSIVE IndexOf(_, _)
IndexOf(seq, ele) ==
  IF seq = <<>> THEN 0
  ELSE IF Head(seq) = ele THEN 1
  ELSE LET i == IndexOf(Tail(seq), ele) IN
       IF i = 0 THEN 0 ELSE i + 1
RECURSIVE Remove(_, _)
Remove(seq, set) ==
  IF Len(seq) = 0 THEN seq
  ELSE (
       (IF Head(seq) \in set THEN <<>> ELSE <<Head(seq)>>)
    \o Remove(Tail(seq), set))
Reinsert(seq, fromIndex, toIndex) ==
  IF toIndex >= fromIndex
  THEN LET elem == seq[fromIndex]
           withoutEleSeq ==
                SubSeq(seq, 1, fromIndex - 1)
             \o SubSeq(seq, fromIndex + 1, Len(seq))
       IN   SubSeq(withoutEleSeq, 1, toIndex - 1)
         \o <<elem>>
         \o SubSeq(withoutEleSeq, toIndex, Len(withoutEleSeq))
  ELSE Assert(FALSE, "toIndex must be greater than or equal to fromIndex.")

NodeSet == inodes \cup {root}
IsParent(p, c) == <<p, c>> \in parent
RECURSIVE IsAncestor(_, _)
IsAncestor(a, d) ==
  \/ IsParent(a, d)
  \/ (\E p \in NodeSet: IsParent(a, p) /\ IsAncestor(p, d))
IsSelfOrAncestor(sa, d) ==
  \/ sa = d
  \/ IsAncestor(sa, d)
IsDescendant(d, a) == IsAncestor(a, d)
IsSelfOrDescendant(sd, a) == IsDescendant(sd, a) \/ sd = a

CalcRenAffXattr(n) ==
  LET ancestors == {a \in NodeSet: IsSelfOrAncestor(a, n)}
      filteredSeq == SelectSeq(modOrder, LAMBDA x: x[1] \in ancestors)
      len == Len(filteredSeq)
  IN IF len = 0
     THEN null
     ELSE actRenAffXattr[filteredSeq[len][1]]

RECURSIVE GetNonRenXattrModIDR(_, _, _)
GetNonRenXattrModIDR(n, renameID, setXattrID) ==
  IF ~IsAncestor(root, n) THEN setXattrID
  ELSE LET p == CHOOSE x \in NodeSet: IsParent(x, n)
           parentRenameID == IndexOf(modOrder, <<p, rename>>)
           parentSetXattrID == IndexOf(modOrder, <<p, setxattr>>)
           maxRenameID == Max({parentRenameID, renameID})
           maxSetXattrID == IF parentSetXattrID > Max({setXattrID, renameID})
                            THEN parentSetXattrID
                            ELSE setXattrID
       IN GetNonRenXattrModIDR(p, maxRenameID, maxSetXattrID)
GetNonRenXattrModID(n) ==
  LET renameID == IndexOf(modOrder, <<n, rename>>)
      setXattrID == IndexOf(modOrder, <<n, setxattr>>)
  IN GetNonRenXattrModIDR(n, renameID, setXattrID)
CalcNonRenAffXattr(n) ==
  LET id == GetNonRenXattrModID(n)
  IN IF id = 0
     THEN null
     ELSE actNonRenAffXattr[modOrder[id][1]]

Init ==
  /\ parent = {}
  /\ expRenAffXattr = [n \in NodeSet |-> null]
  /\ actRenAffXattr = [n \in NodeSet |-> null]
  /\ expNonRenAffXattr = [n \in NodeSet |-> null]
  /\ actNonRenAffXattr = [n \in NodeSet |-> null]
  /\ modOrder = <<>>

Create(n, p) ==
  /\ ~IsDescendant(n, root)
  /\ IsSelfOrDescendant(p, root)
  /\ parent' = parent \cup {<<p, n>>}
  /\ expRenAffXattr' = [expRenAffXattr EXCEPT ![n] = expRenAffXattr[p]]
  /\ actRenAffXattr' = [actRenAffXattr EXCEPT ![n] = CalcRenAffXattr(p)]
  /\ UNCHANGED <<expNonRenAffXattr, actNonRenAffXattr>>
  /\ modOrder' = Append(Append(modOrder, <<n, rename>>), <<n, setxattr>>)
Rename(n, p1, p2) ==
  /\ IsSelfOrDescendant(p1, root)
  /\ IsSelfOrDescendant(p2, root)
  /\ IsParent(p1, n)
  /\ ~IsSelfOrAncestor(n, p2)
  /\ parent' = (parent \ {<<p1, n>>}) \union {<<p2, n>>}
  /\ expRenAffXattr' = [x \in NodeSet |->
                          IF IsSelfOrDescendant(x, n)
                          THEN expRenAffXattr[p2]
                          ELSE expRenAffXattr[x]]
  /\ actRenAffXattr' = [actRenAffXattr EXCEPT ![n] = CalcRenAffXattr(p2)]
  /\ UNCHANGED <<expNonRenAffXattr>>
  /\ actNonRenAffXattr' = [actNonRenAffXattr EXCEPT ![n] = CalcNonRenAffXattr(n)]
  /\ modOrder' =
       Append(
         Remove(
           Reinsert(modOrder,
                    IndexOf(modOrder, <<n, setxattr>>),
                    GetNonRenXattrModID(n)),
           {<<n, rename>>}),
         <<n, rename>>)
  /\ LET i == IndexOf(modOrder', <<n, setxattr>>)
         j == IndexOf(modOrder', <<modOrder[GetNonRenXattrModID(n)][1], setxattr>>)
     IN Assert(i = j \/ i = j + 1,
               "n's setxattr should be directly after its latest ancestor's setxattr.")
Delete(n) ==
  LET descendants == {x \in NodeSet: IsSelfOrDescendant(x, n)} IN
  /\ IsDescendant(n, root)
  /\ parent' = {<<p, c>> \in parent: ~IsDescendant(c, n) /\ c # n}
  /\ expRenAffXattr' = [x \in NodeSet |->
                          IF IsSelfOrDescendant(x, n)
                          THEN null
                          ELSE expRenAffXattr[x]]
  /\ actRenAffXattr' = [x \in NodeSet |->
                          IF IsSelfOrDescendant(x, n)
                          THEN null
                          ELSE actRenAffXattr[x]]
  /\ expNonRenAffXattr' = [x \in NodeSet |->
                             IF IsSelfOrDescendant(x, n)
                             THEN null
                             ELSE expNonRenAffXattr[x]]
  /\ actNonRenAffXattr' = [x \in NodeSet |->
                             IF IsSelfOrDescendant(x, n)
                             THEN null
                             ELSE actNonRenAffXattr[x]]
  /\ modOrder' =
       Remove(
         modOrder,
         {x \in inodes: IsSelfOrDescendant(x, n)} \times operations)
SetXattr(n, v) ==
  /\ IsDescendant(n, root)
  /\ expRenAffXattr' = [x \in NodeSet |->
                         IF IsSelfOrDescendant(x, n) THEN v
                         ELSE expRenAffXattr[x]]
  /\ actRenAffXattr' = [actRenAffXattr EXCEPT ![n] = v]
  /\ expNonRenAffXattr' = [x \in NodeSet |->
                            IF IsSelfOrDescendant(x, n) THEN v
                            ELSE expNonRenAffXattr[x]]
  /\ actNonRenAffXattr' = [actNonRenAffXattr EXCEPT ![n] = v]
  /\ modOrder' = Append(Remove(modOrder, {<<n, setxattr>>}), <<n, setxattr>>)
  /\ UNCHANGED <<parent>>
Next ==
  \/ \E n \in inodes, p \in NodeSet: Create(n, p)
  \/ \E n \in inodes, p1, p2 \in NodeSet: Rename(n, p1, p2)
  \/ \E n \in inodes: Delete(n)
  \/ \E n \in inodes, v \in values: SetXattr(n, v)

Spec ==
  /\ Init
  /\ [][Next]_<<parent,
               expRenAffXattr, actRenAffXattr,
               expNonRenAffXattr, actNonRenAffXattr,
               modOrder>>

TypeOK ==
  /\ \A <<p, c>> \in parent:
      p \in NodeSet /\ c \in inodes /\ IsSelfOrDescendant(p, root)
  /\ expRenAffXattr \in [NodeSet -> values]
  /\ actRenAffXattr \in [NodeSet -> values]
  /\ expNonRenAffXattr \in [NodeSet -> values]
  /\ actNonRenAffXattr \in [NodeSet -> values]
  /\ modOrder \in Seq(inodes \times operations)
  /\ \A n \in inodes:
          (IndexOf(modOrder, <<n, rename>>) # 0 /\ IndexOf(modOrder, <<n, setxattr>>) # 0)
      <=> IsDescendant(n, root)
  /\ \A n \in inodes, op \in operations:
       \A i, j \in 1..Len(modOrder):
         (modOrder[i] = <<n, op>> /\ modOrder[j] = <<n, op>>) => i = j

Consistent ==
  /\ \A n \in NodeSet: CalcRenAffXattr(n) = expRenAffXattr[n]
  /\ \A n \in NodeSet: CalcNonRenAffXattr(n) = expNonRenAffXattr[n]

Invariant ==
  /\ TypeOK
  /\ Consistent
==============================================================================================

\* Xattr.cfg
CONSTANT
root = root
inodes = {a, b, c, d}
null = null
blue = blue
green = green
values = {null, blue, green}
rename = rename
setxattr = setxattr
operations = {rename, setxattr}

SYMMETRY
SYMM

SPECIFICATION
Spec

INVARIANT
Invariant

# java -Xms60g -XX:+UseParallelGC -XX:MaxDirectMemorySize=60g -Dtlc2.tool.fp.FPSet.impl=tlc2.tool.fp.OffHeapDiskFPSet -cp /usr/local/lib/tla2tools.jar tlc2.TLC Xattr -workers auto -checkpoint 0
Model checking completed. No error has been found.
  Estimates of the probability that TLC did not check all reachable states
  because two distinct states had the same fingerprint:
  calculated (optimistic):  val = .0010
  based on the actual fingerprints:  val = 3.4E-6
740384039 states generated, 26449486 distinct states found, 0 states left on queue.
The depth of the complete state graph search is 19.
The average outdegree of the complete state graph is 1 (minimum is 0, the maximum 25 and the 95th percentile is 5).
Finished in 01h 25min at (2024-10-17 00:34:40)

Proposing Enhancements for Data Movement

Some xattrs, such as storage policies, can affect data placement. HDFS proposes a storage policy satisfier that performs data movement based on recursive scanning to fulfill storage policies. However, it has a shortcoming: if the active namenode fails over during the process, it must rescan from the beginning. To overcome this, we propose:

• For newly created files, calculate the exact xattr using the above method and choose block locations based on the resolved xattr.
• For renamed directories or files, if their xattr does not match the xattr after renaming, generate an index to inform the satisfier that this subtree needs handling.
• For setxattr operations that change the xattr of a subtree, also generate an index to inform the satisfier.
• The xattr satisfier scans the subtree indicated by the indices. When scanning a node, after setting the actual xattr of all immediate children to the expected xattr (note: if a child's actual xattr and expected xattr do not match, generate a new index), remove the corresponding index for that node.

With this approach, each inode is scanned at most once, even if a namenode failover occurs.