Paper Interpretation - There Is More Consensus In Egalitarian Parliaments
This post is the first in a series on EPaxos, focusing specifically on Simplified Egalitarian Paxos. In subsequent posts, I'll delve into Optimized Egalitarian Paxos along with its safety and liveness properties, and explore how Linearizability and Serializability are achieved in Egalitarian Paxos. Additionally, I plan to demonstrate how to transition from Fast Paxos to EPaxos using TLA+ in future posts.
The Commit Protocol: Transitioning from Fast Paxos to Egalitarian Paxos
The commentary by drdr.xp on xiangguangyan's article EPaxos Trilogy II: EPaxos Core Protocol Process provides valuable insight into the transition from Fast Paxos to Egalitarian Paxos:
The distinction between a fast quorum (or perhaps "fast path" is a more precise term?) and Fast Paxos is essentially non-existent.
We should do the following minor changes to Fast Paxos:
- In fast round, the acceptors will do some minor changes to value, make it \(w\).
- Unify all states to cmds.
- Change message path.
I have gained a comprehensive understanding of the classic Paxos algorithm through The Part-Time Parliament, and of the Fast Paxos algorithm through Fast Paxos. However, I've noticed that the terminology used in these papers differs from that used in this paper. To ease the transition and ensure clarity, I've compiled a table aligning the terminologies from all these sources. Notably, in this section, I will use the terms "coordinators" and "replicas" interchangeably when they act as designated leaders, and similarly, "acceptors" and "replicas" will also be used interchangeably.
| The Part-Time Parliament | Fast Paxos | EPaxos |
|---|---|---|
| priests | coordinators | replicas, designated leaders |
| priests | acceptors | replicas |
| priests | proposers | replicas, designated leaders |
| priests | learners | replicas, designated leaders |
| ballot | round | ballot |
| \(\operatorname{nextBal}(p)\) | \(\operatorname{rnd}(a)\) | \(\operatorname{cmds}_L[L][i_L]\) |
| \({\operatorname{prevVote}(p)}_{bal}\) | \(\operatorname{vrnd}(a)\) | \(\operatorname{cmds}_Q[L][i_L]\) |
| \({\operatorname{prevVote}(p)}_{dec}\) | \(\operatorname{vval}(a)\) | \(\operatorname{cmds}_Q[L][i_L]\) |
| \(\operatorname{lastTried}(p)\) | \(\operatorname{crnd}(c)\) | \(\operatorname{cmds}_L[L][i_L]\) |
| \(\operatorname{cval}(c)\) | \(\operatorname{cmds}_L[L][i_L]\) | |
| Step 1 of the Basic Protocol | phase 1a | Explicit Prepare |
| \(\operatorname{NextBallot}(b)\) | phase 1a message | \(\operatorname{Prepare}(epoch.(b+1).Q, L.i)\) |
| Step 2 of the Basic Protocol | phase 1b | Explicit Prepare |
| \(\operatorname{LastVote}(b, v)\) | phase 1b message | \(\operatorname{PrepareOK}(\operatorname{cmds}_R[L][i], epoch.x.Y, L.i)\) |
| Step 3 of the Basic Protocol | phase 2a | Paxos-Accept |
| \(\operatorname{BeginBallot}(b, d)\) | phase 2a message | \(\operatorname{Accept}(\gamma, \text{seq}_\gamma, \text{deps}_\gamma, L.i)\) |
| Step 4 of the Basic Protocol | phase 2b | Paxos-Accept |
| \(\operatorname{Voted}(b, q)\) | phase 2b message | \(\operatorname{AcceptOK}(\gamma, L.i)\) |
Bypass "Any" Messages in Fast Rounds
In Fast Paxos, during a fast round \(i\), if the coordinator can pick any proposed value in phase 2a, then instead of picking a single value, it may instead send a special phase 2a message called an any message to the acceptors. When an acceptor receives a phase 2a any message, it may treat any proposer's message proposing a value as if it were an ordinary round \(i\) phase 2a message with that value.
Moving on to Egalitarian Paxos, each instance is associated with a predefined instance sub-space. Only specific instances can propose the minimum ballot of each instance. With this knowledge, the coordinator understands that it can select any proposed value in the minimum ballot, even if it bypasses phase1a and phase1b. Similarly, the acceptors realize they can treat any proposer's message proposing a value as if it were a ordinary phase 2a message, without the explicit requirement of receiving an "any" message.
Unoptimized Coordinated Collision Recovery
In Fast Paxos, the obvious way to recover from a collision is for \(c\) to begin a new round, sending phase 1a messages to all acceptors, if it learns that round \(i\) may not have chosen a value. Suppose the coordinator \(c\) of round \(i\) is also coordinator of round \(i + 1\), and that round \(i + 1\) is the new one it starts. The phase 1b message that an acceptor a sends in response to \(c\)'s round \(i + 1\) phase 1a message does two things: it reports the current values of \(\operatorname{vrnd}(a)\) and \(\operatorname{vval}(a)\), and it transmits \(a\)'s promise not to cast any further vote in any round numbered less than \(i + 1\). (This promise is implicit in \(a\)'s setting \(\operatorname{rnd}(a)\) to \(i + 1\).)
Fast Paxos introduces an optimized approach for collision recovery. However, the Explicit Prepare phase in Egalitarian Paxos starkly resembles an unrefined, straightforward method for handling collisions, which lacks optimization:

Does the Acceptor Promise to Avoid Voting for Ballots with Lower IDs When Responding to "Prepare" Messages?
Yes, the Acceptor promises not to vote for ballots with lower IDs when responding to \(Prepare\) messages.
The above recovery procedure is a simplified version, and it omits a critical detail. For a more thorough and precise understanding, let's reference the TLA+ specification from A Proof of Correctness for Egalitarian Paxos:
1 | |
The condition msg.ballot[1] > rec.ballot[1] ensures that an acceptor will only respond to a prepare message if the ballot ID of the prepare message is greater than that of the preceding message. This response mechanism mirrors the phase 1b of Fast Paxos: If an acceptor \(a\) receives a request to participate in round \(i\) and \(i > \operatorname{rnd}(a)\), then \(a\) sets \(\operatorname{rnd}(a)\) to \(i\) and sends coordinator \(c\) a message containing the round number \(i\) and the current values of \(\operatorname{vrnd}(a)\) and \(\operatorname{vval}(a)\). If \(i \le \operatorname{rnd}(a)\) (so \(a\) has begun round \(i\) or a higher-numbered round), then \(a\) ignores the request.
1 | |
An acceptor should abstain from initially accepting a value and then subsequently pre-accepting a different value with the same ballot ID. This behavior deviates from the Fast Paxos protocol and could potentially jeopardize the accuracy of the recovery process. EPaxos addresses this issue in a subtle manner: after receiving and processing a pre-accept message, the acceptor removes it from sentMsg to avoid processing it repeatedly. Furthermore, the coordinator is designed to not send pre-accept and accept messages with the same ballot ID in an unexpected order. This mechanism ensures that an acceptor will not initially accept a value and then subsequently pre-accept a different value with an identical ballot ID.
While the strategy of removing processed messages from sentMsg serves its purpose, it might be deemed as excessively complex or counter-intuitive. A more straightforward and potentially intuitive approach to achieving the same result might involve ensuring that the acceptor's status is not set to "accepted".
Selecting Values Based on Observation 4
In EPaxos, it is assumed that every fast quorum includes \(2F = N - 1\) replicas and every slow quorum contains \(F + 1 = \lfloor N / 2\rfloor + 1\) replicas. This quorum configuration satisfies the Quorum Requirement: If \(j\) is a fast round number, then any \(i\)-quorum intersects with any two \(j\)-quorums, as evidenced by the equation \((2F + 2F - (2F + 1)) + (F + 1) - (2F + 1) = F - 1\).
Assuming a fast quorum with \(2F\) acceptors and a slow quorum with \(F + 1 = \lfloor N / 2\rfloor + 1\) acceptors, the fast quorum is required to intersect with the slow quorum, containing at least \(2F + (F + 1) - (2F + 1) = F = \lfloor N / 2\rfloor\) acceptors. This can also be expressed as: if there are \(2F + (F + 1) - (2F + 1) = F = \lfloor N / 2\rfloor\) acceptors' replies, each containing identical values in response to \(Prepare\) messages and accepted by the coordinator, then there must be at least one fast quorum and one slow quorum, the intersection of which exactly comprises these acceptors. The statements on Lines 32 and 33 of Figure 3, which describes the EPaxos simplified recovery procedure, mirrors a basic and unoptimized approach for Coordinated Collision Recovery in Fast Paxos.
The statement in Line 32, which involves value selection, mirrors Observation 4 in Fast Paxos: With \(Q\), \(vr\), \(vv\), and \(k\) as in Figure 1, a value \(v\) has been or might yet be chosen in round \(k\) iff there exists a \(k\)-quorum \(R\) such that \(\operatorname{vr}(a) = k\) and \(\operatorname{vv}(a) = v\) for all acceptors \(a\) in \(R \cap Q\).

The statement in Line 33, which initiates the Paxos-Accept phase, closely reflects Phase 2 in Fast Paxos. Consider a new ballot ID that includes the phase name, such as \(epoch.b.Q.prepare\) and \(epoch.b.Q.accept\), with \(epoch.b.Q.accept > epoch.b.Q.prepare\). Under this consideration, the EPaxos simplified recovery procedure can be viewed as corresponding to Phase 1 and Phase 2 of Fast Paxos.
Why does Line 32 specifically emphasize the condition concerning "replies for the default ballot"?
Let \(\mathcal{R}\) represent the set of replies associated with the highest ballot number \(i\). Firstly, I believe the authors highlight Lines 32 and 33 to address situations where the prior round \(i\) is a fast round. If the previous round \(i\) is a slow round, Lines 28, 30, or 34 are intended to handle it. Secondly, if Lines 35 and 37 were to send a different type of messages (such as \(TryPreaccept\) messages), and reserve \(PreAccept\) messages and their replies exclusively for the fast round, it appears that removing this condition would not jeopardize the correctness of EPaxos.
Why does Line 32 specifically emphasize the condition concerning "none of those replies is from \(L\)"?
A Proof of Correctness for Egalitarian Paxos provides an answer:
Since \(b_1\) is successful after Phase 1 , then a fast quorum (\(N - 1\) replicas) have recorded the same tuple \(\left(\gamma, \text{seq}_\gamma, \text{deps}_\gamma\right)\) for instance \(Q.i\). For \(b_2\) to start, its leader must receive replies to Prepare messages from at least \(\lfloor N / 2\rfloor + 1\) replicas. Therefore, at least \(\lfloor N / 2\rfloor\) replicas will see a Prepare for \(b_2\) after they have recorded \(\left(\gamma, \text{seq}_\gamma, \text{deps}_\gamma\right)\) for ballot \(b_1\) (if they had seen the larger ballot \(b_2\) first, they would not have acknowledged any message for ballot \(b_1\)). \(b_2\)'s leader will therefore receive at least \(\lfloor N / 2\rfloor\) \(PrepareReply\)'s with tuple \(\left(\gamma, \text{seq}_\gamma, \text{deps}_\gamma\right)\) marked as pre-accepted.
If the leader of \(b_1\) is among the replicas that reply to the Prepare of ballot \(b_2\), then it must have replied after the end of Phase 1 (otherwise it couldn't have completed the smaller ballot \(b_1\)), so it will have committed tuple \(\left(\gamma, \text{seq}_\gamma, \text{deps}_\gamma\right)\) by then. The leader of \(b_2\) will then know it is safe to commit the same tuple.
Below, we assume that the leader of \(b_1\) is not among the replicas that reply to the Prepare of ballot \(b_2\).
Pay attention to the use of must. The author clarifies that under EPaxos protocol, the leader should refrain from replying to \(Prepare\) messages until the commitment in the fast round is finalized. Thus, if the leader in \(b_2\) receives a response to the \(Prepare\) message, the response must contain the committed state. This situation will be addressed by lines 28 and 29. Therefore, eliminating the condition related to "none of those replies is from \(L\)" will not jeopardize the correctness of the EPaxos protocol.
Selecting Values Based on the Presence of an "Accepted" Reply Message
Let \(\mathcal{R}\) represent the set of replies associated with the highest ballot number \(i\). Suppose \(\mathcal{R}\) contains a reply from an acceptor indicating that it has accepted the value \(v\) during Phase 2 (Paxos-Accept). Given that the ballot with the highest number \(i\) corresponds to a slow round (analogous to the slow path in EPaxos), we can infer that the coordinator proposed the specific value \(v\) by sending phase2a messages. Consequently, the acceptors selected \(v\) in response to these phase2a messages during the slow round \(i\). We can then conclude that all acceptors either accepted nothing or accepted \(v\) only. Therefore, either no value was committed during that slow round, or the specific value \(v\) was committed. As a result, \(v\) can be selected as the value for a new round with a ballot ID higher than \(i\).
In fact, I believe that enabling the coordinator to propose the value \(v\) directly, upon learning that it has been accepted in a slow round with a lower ballot ID, could be a viable optimization for Fast Paxos. I plan to modify the TLA+ specification of Fast Paxos to incorporate this change and then verify it.
The key part of this optimization is enabling the acceptor to distinguish whether it has accepted the value \(v\) in a fast round or a slow round. EPaxos effectively illustrates this approach by differentiating these cases using a "status" field (pre-accepted", "accepted").
Selecting Values Based on the Presence of an "Committed" Reply Message
In The Part-Time Parliament, Theorem 1 establishes that any two successful ballots are for the same decree. Upon encountering a "Committed" reply message, we can deduce that the value \(v\) is committed. Given the assurance of Theorem 1, no other value has been, or will be, committed. Thus, it's safe to commit the value \(v\) once more.
Optimized Coordinated Collision Recovery
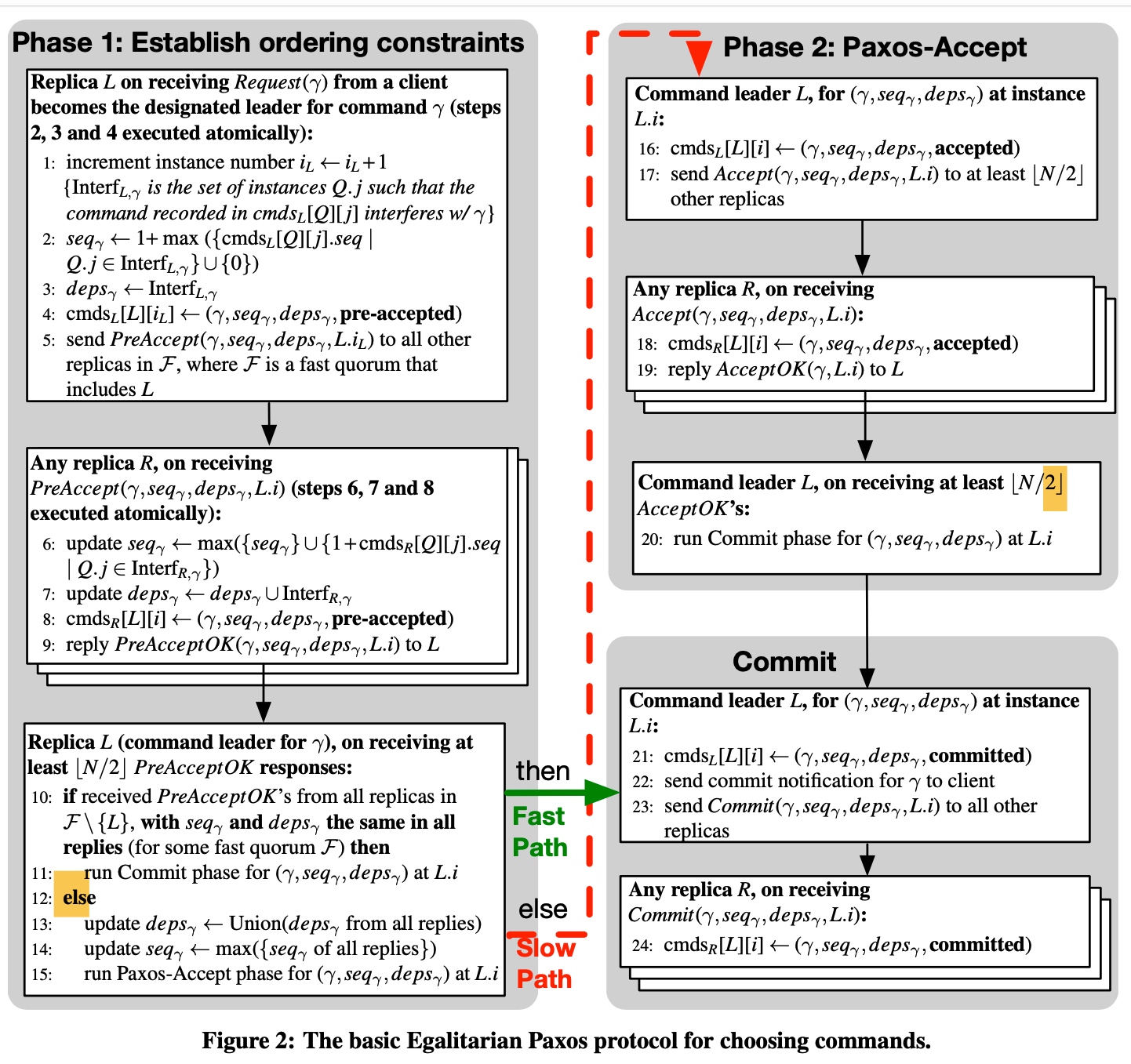
In Fast Paxos, the author introduces an observation: In other words, \(a\)'s round \(i\) phase 2b message carries exactly the same information as its round \(i + 1\) phase 1b message. Specifically, both messages accomplish two key tasks: they report the current values of \(\operatorname{vrnd}(a)\) and \(\operatorname{vval}(a)\), and they transmit \(a\)'s promise not to cast any further vote in any round numbered less than \(i + 1\). This observation leads to the optimized coordinated collision recovery. EPaxos also employs the same optimized coordinated collision recovery approach, which corresponds to the segment between the two yellow-highlighted sections in the above figure, labeled as "Figure 2: The Basic Egalitarian Paxos Protocol for Choosing Commands".
It's important to note that in the Paxos-Accept phase, the command leader \(L\) always sends an \(\operatorname{AcceptOK}(\gamma, L.i)\) "reply" to itself, as demonstrated in line 16. Consequently, the command leader \(L\) can proceed to the commit phase after receiving only \(\lfloor N / 2\rfloor\) \(\operatorname{AcceptOK}\) messages, rather than needing to wait for \(\lfloor N / 2\rfloor + 1\).
Overlooked Details
A Closer Look at Ballot Numbers and Instance Numbers
For correctness, ballot numbers used by different replicas must be distinct, so they include a replica ID. Actually, the uniqueness of ballot numbers originates from the \(\operatorname{B1}(\mathcal{B})\) condition in The Part-Time Parliament. Furthermore, a newer configuration of the replica set must have strict precedence over an older one, so we also prepend an epoch number. The resulting ballot number format is \(epoch.b.R\), where a replica \(R\) increments only the natural number \(b\) when trying to initiate a new ballot in Explicit Prepare. Each replica is the default (i.e., initial) leader of its own instances, so the ballot \(epoch.0.R\) is implicit at the beginning of every instance \(R.i\).
For every replica \(R\) there is an unbounded sequence of numbered instances \(R.1\), \(R.2\), \(R.3\), ... that that replica is said to own.
Understanding the Lack of Transitivity in Interference Relations
Two commands \(\gamma\) and \(\delta\) interfere if there exists a sequence of commands \(\Sigma\) such that the serial execution \(\Sigma, \gamma, \delta\) is not compatible (i.e., it produces different results than) the serial execution \(\Sigma, \delta, \gamma\).
EPaxos guarantees that any two interfering commands will be executed in the same order with respect to each other on every replica. This is enough to guarantee that the executions on all replicas are compatible: the serial ordering of commands on a replica can be obtained from that on any other replica by commuting commutative commands.
Note that the interference relation is symmetric, but not necessarily transitive.
While the authors of EPaxos propose that the interference relation need not be transitive, I argue that this assumption lacks practical utility in real-world systems and is, in fact, counter-intuitive. It appears the authors intended to simplify the process of demonstrating execution consistency, defined as the principle where two interfering commands, \(\gamma\) and \(\delta\), when successfully committed (not necessarily by the same replica), are executed in the same order by every replica. The partial proof for execution consistency, specifically within the realm of the commit protocol, is laid out as follows:
- The attributes with which a command \(c\) is committed are the union of at least \(\lfloor N / 2\rfloor + 1\) sets of attributes computed by as many replicas. This ensures that there is at least one replica \(R\) that contributes to both the final attributes of \(\gamma\) and \(\delta\).
- Because \(R\) records every command that it sees in its command log, and because \(\gamma \sim \delta\), \(R\) will include the command it sees first in the dependency list of the command it sees second. In other words, if \(\gamma\) and \(\delta\) are successfully committed and \(\gamma \sim \delta\), then either \(\gamma\) has \(\delta\) in its dependency list when \(\gamma\) is committed, or \(\delta\) has \(\gamma\) in its dependency list when \(\delta\) is committed.
Calculation of Fast Quorum and Slow Quorum Sizes
Let's denote the fast quorum size as \(F\), the slow quorum size as \(S\), and the replicas size as \(N\). In accordance with the Quorum Requirement, we must ensure that \(((F + F) - N) + S - N \ge 1\). Additionally, the \(\operatorname{B2}(\mathcal{B})\) condition dictates that \(S + S - N \ge 1\). From these conditions, we can easily compute the minimum value for \(S\) as \(S = \lfloor N / 2\rfloor + 1\). Similarly, the minimum value for \(F\) can be determined as \(F = \lceil 3 N / 4\rceil\).
The Execution Algorithm
To execute command \(\gamma\) committed in instance \(R.i\), a replica will follow these steps:
- Wait for \(R.i\) to be committed (or run Explicit Prepare to force it);
- Build \(\gamma\)'s dependency graph by adding \(\gamma\) and all commands in instances from \(\gamma\)'s dependency list as nodes, with directed edges from \(\gamma\) to these nodes, repeating this process recursively for all of \(\gamma\)'s dependencies (starting with step 1);
- Find the strongly connected components, sort them topologically;
- In inverse topological order, for each strongly connected component, do:
- Sort all commands in the strongly connected component by their sequence number;
- Execute every un-executed command in increasing sequence number order, marking them executed.